一个数据在一个节点需要同步到另外一个节点的过程中,在未完成同步的时候,会出现数据不一致的情况,所以此时必然存在分区容错性(Partition tolerance)。分布式系统只能从一致性(Consistency)或可用性(Availability)之间去选择。
CAP讲的是分布式一致性,而这次我们来聊聊分布式共识性。很多开发者一直以为一致性与共识性是同一个东西,但两者讲的是完全不同的东西。
- 一致性:A点同步B点数据,然后两者之间的数据可以达成一致。
- 共识性:一个或多个节点提议了一个值应当是什么后,采用一种大家都认可的方法,使得系统中所有进程对这个值达成一致意见。

共识性比较常见的场景就是选主,例如redis主挂掉了,集群通用共识性算法选出一个主。比特币之类的电子货币也需要更复杂的共识性算法。
下面我们一步步聊下分布式共识性的一些常见算法与问题。
拜占庭将军问题
Leslie Lamport(论文排版系统LaTeX的开发者,同时也是2013年的图灵奖得主)在其论文中描述了如下系统:
一组拜占庭将军分别各率领一支军队共同围困一座城市。
为了简化模型,将各支军队的行动策略限定为进攻或撤离两种。因为部分军队进攻部分军队撤离可能会造成灾难性后果,因此各位将军必须通过投票来达成一致策略,即所有军队一起进攻或所有军队一起撤离。
同时各位将军分处城市不同方向,他们只能通过信使互相联系。在投票过程中每位将军都将自己投票给进攻还是撤退的信息通过信使分别通知其他所有将军,这样一来每位将军根据自己的投票和其他所有将军送来的信息就可以知道共同的投票结果而决定行动策略。
此系统的名字叫做拜占庭将军问题。从描述中,可以显然知道,将军们需要通过少数服从多数的算法在分布式的场景下进行投票决议一个一致性的决定去执行。
在拜占庭将军问题中,默认是认为信使是不会被截获并且消息会传递到的。更多的情况中,将军中可能会出现叛徒、信使会被截获冒充、消息无法到达。而叛徒或信使冒充会恶意地向其他将军投票,给不同将军展示不同的投票结果,从而破坏了将军们执行的一致性。而此类错误则称为拜占庭错误。
如果系统能处理拜占庭将军错误正常运行的话,则称系统拥有拜占庭容错「Byzantine fault tolerance」,简称为BFT。
举个例子
假设当时有5位将军投票(单数投票的结果必能形成少数服从多数),其中有1名是叛徒,4名忠诚的将军中出2人投进攻,2人投撤离的。
这时候叛徒可能故意给2名投进攻的将军送信表示投进攻,而给另外2名投撤离的将军送信表示投撤离。这样在2名投进攻的将领看来,投票结果是3人投进攻,从而发起进攻;而在2名投撤离的将军看来则是3人投撤离。这样各支军队的一致协同就遭到了破坏,结果是灾难性的。
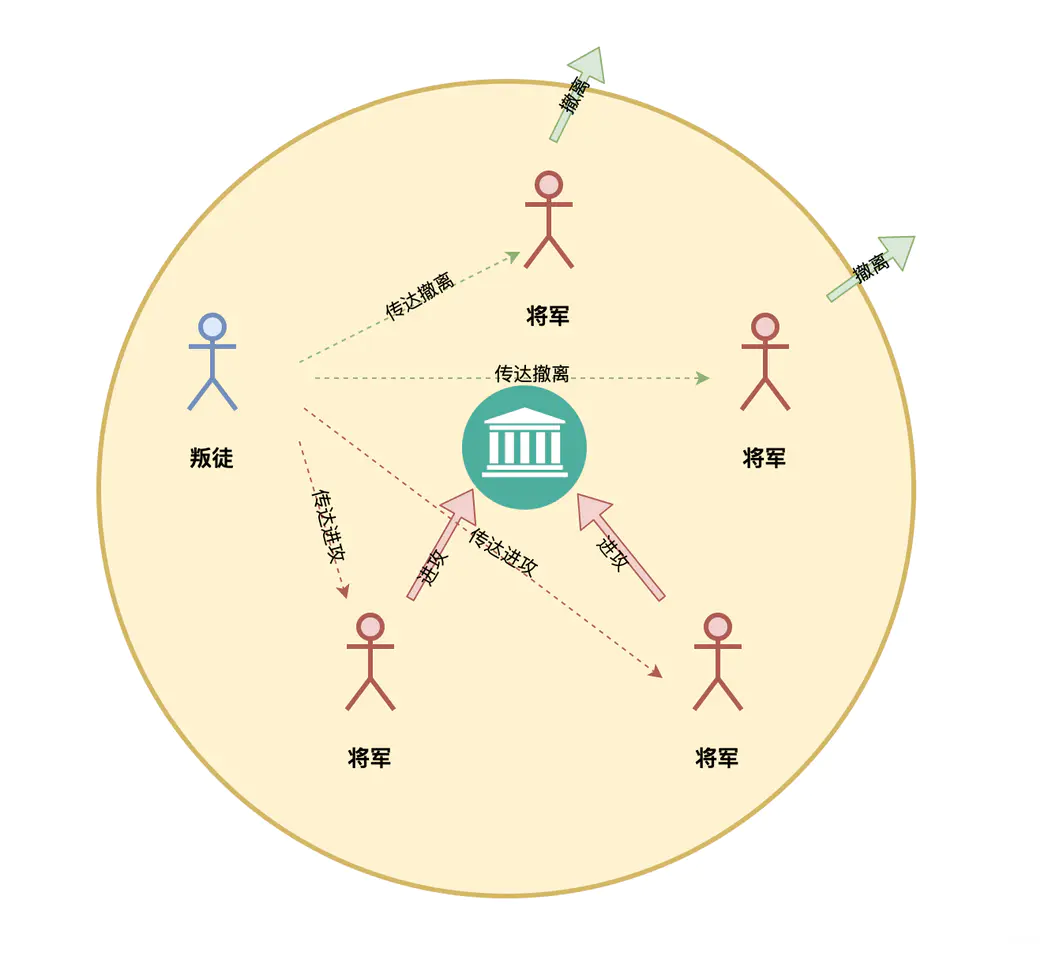
即使这5个将军都是忠诚的,但投票结果是需要信使在将军之间去传递的,而这些信使在传递过程中是有可能被截冒充或者并没有传递到将军的投票结果,最终还是会影响军队的一致协同。
上述的故事映射到计算机系统中,将军便成了计算机,而信使则是通信系统。有人会觉得这个问题可以通过加密或签名的方式解决,但本质上加密过程、签名算法也会出错。虽然加密和签名一定程度是可以解决这个问题,但这个问题并不是要讨论这些加密签名的强度,而是更多地在于研究集群系统客观上已经出现错误了,他们要怎么在存在错误的情况下让系统正常的工作。
经典的简单解决
首先要知道,为什么这个标题是经典的简单解决?因为这个解决只是个简单的解决,在现代系统很多场景中,并不具有普遍的解决能力。
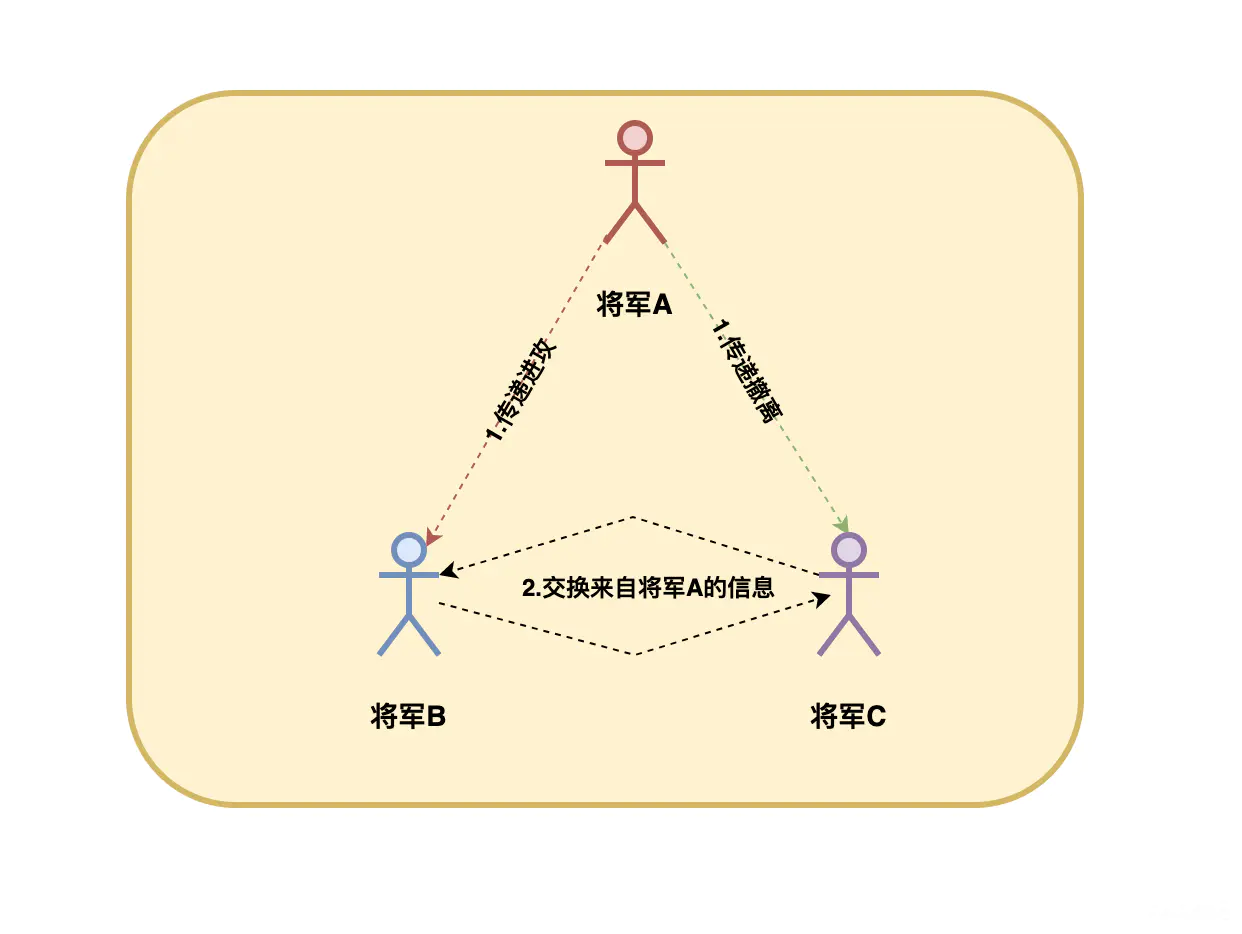
大家看完上面的例子,可能会涌现一种想法,就是在收到来自同一个将军的投票后,交换各自的结果检验看该将军是否叛徒。例如A将军把进攻指令发给B将军,把撤离指令发给C将军,那么BC将军交互一下来自A将军的指令,就可以知道A将军是个叛徒,然后把他揪出来干掉,不再听他的指令。
但是这种做法根本不能解决问题。虽然在BC交换指令后,可以知道有叛徒的存在,但其实你并不能确定A就是叛徒,因为有可能BC交换指令的过程出现”拜错“,所以上面的思路并不能解决问题。
回到问题本身,我们是需要在存在错误的情况下让系统正常进行,所以我们只需要设计一套系统在兼容这些”叛徒“就足够了。怎么理解?回到拜占庭军队上,拜占庭军队攻下一座城池至少需要6个将军,那么让军队装备更多将军,例如10个,在通过两两交互指令验证完消息后,可以知道有多少个叛徒的存在。只要忠诚的将军数大于等于6那么就可以执行指令(进攻或撤离),否则军队则按兵不动。这个容错率可以根据自己的系统进行设置,在这个方案被提出时,容错率描述是1/3。
开头也说到这个方案在现代系统并不具有普遍解决问题的能力。一是类似比特币这种分布式记账本千千万个节点,如果要进行两两的信息验证,这个过程和开销是非常大的,会变得不实际。另外就是并不是所有性质的系统都能允许错误节点的执行,例如注册中心、交易中心等。
先进的解决——比特币的工作量证明
在“简单解决”的方案提出之后,有非常多的方案算法被提出,实用拜占庭容错(PBFT)、联邦拜占庭协议(FBA)、授权拜占庭容错算法(dBFT)等等。由于其中的复杂度与文章篇幅问题,不一一赘述,有兴趣可以到网上查阅。
但其中一个比较有意思的是比特币中所用到的工作量证明「Proof Of Work,POW」可以大概提一下。
工作量证明是一种对应服务与资源滥用、或是拒绝服务攻击的经济对策。一般是要求用户进行一些耗时适当的复杂运算,并且答案能被服务方快速验算,以此耗用的时间、设备与能源做为担保成本,以确保服务与资源是被真正的需求所使用。(来自维基百科的解释)

结合比特币的场景去理解,用户是需要通过挖矿来获得比特币,而挖矿是需要花费大量的计算资源的。这个挖矿的过程其实是比特币设计的一道解密算法,用户(节点)是需要一定量的计算才能获得答案,然后其他给节点验算,成功后最终获得比特币奖励争取记账权。一句话概括工作量证明就是不校验你的过程,只看你的结果,但获取这个结果是有壁垒的。具体的算法原理在后续讲到共识性算法的应用我们再用新篇幅去阐述。
那么比特币怎样才能造假呢?其实它本质依然是少数服从多数的投票,节点获取结果后是需要其他节点进行验证投票的,如果你拥有大于50%的假节点,的确是可以篡改数据,控制交易。但是工作量证明引入使得构造一个节点的成本已经足够大了,在千千万的节点下想要构造大于50%的假节点,估计有这种财力去实现的人已经可以统治地球了。
拜占庭将军错误看似一个非常严重的问题,能造成灾难性后果,但其实在大部分场景下并不会出现“拜错”。下一篇将会落到比较应用层面的共识性算法,聊下市面上主流的分布式中间件是怎么在不考虑“拜错”的情况下,解决分布式共识性问题的。
备注
摘自:拜占庭问题
